MHT CET Maths Syllabus 2025: Download PDF, Weightage

MHT CET Maths syllabus 2025 includes essential topics such as Trigonometric functions, Matrices, Three-dimensional geometry and more. Candidates can download the MHT CET Mathematics syllabus from the link provided below.

MHT CET Maths syllabus is included in the PCM course. The Mathematics section of the MHT CET 2025 exam will have 150 questions carrying 2 marks each. There will be no negative marking for wrong answers.

MHT CET Maths Syllabus PDF 2025

In the past years, the MHT CET maths syllabus has been changed by the authorities. Candidates can find the link to download the old MHT CET Maths syllabus PDF in the table given below:

MHT CET 2025 Maths Syllabus PDF

Download PDF

MHT CET Maths Syllabus - Deleted Topics

MHT CET maths syllabus was elaborate. Keeping in mind the current scenario, the higher authorities decided to delete certain topics. The entire MHT CET syllabus that is now deleted is mentioned in the PDF. Candidates must check the PDF once before starting the preparation.

Official Deleted Math Syllabus

Download PDF

Also Read: How to Score 150+ in MHT CET 2025 for B.Tech Admission?

MHT CET Maths Topic-Wise Syllabus 2025

The questions included in the Mathematics section of the exam will test the candidates' Mathematical aptitude and problem-solving skills. The topics are given below:

MHT CET Maths Class 11th Topics 2025

The topics in the MHT CET Maths syllabus that are covered in class 11th are given below:

Trigonometric functions

• Need & concept
• Trigonometric functions with the help of standard unit circle
• Signs of trigonometric functions in different quadrants
• Trigonometric functions of particular angles
• Domain and range of trigonometric functions
• Periodicity of functions
• Fundamental identities
• Graphs of trigonometric functions
• Graph of y = a sin bx, y = a cos bx
• Trigonometric functions of negative angles
• Factorization Formulae

• Introduction
• Formulae for conversion of sum or difference into products
• Formulae for conversion of product into sum or difference
• Trigonometric functions of angles of a triangle

Straight Line

• Inclination of a line
• Slope of a line
• Equation of lines parallel to coordinate axes
• Intercepts of a line
• Revision of different forms of equations of a line
• Slope-point form
• Slope-intercept form
• Two point form
• Double intercept form
• Other forms of equations of a line
• Parametric form, normal form, general form

Circle and Conics

• Standard equation
• Centre-radius form
• Diameter form
• General equation
• Parametric equations of standard equation
• Conics Napees
• Application of conic section

Sets, Relations and Functions

• Subset, proper improper subset and their properties
• Union, intersection, disjoint sets, empty set
• Finite & infinite sets, equal sets, equivalent sets, universal set
• Venn diagrams, complement of a set
• Difference of two sets, power set, Relations – ordered pairs, equality of ordered pairs
• Cartesian product of two sets, No. of elements in the Cartesian product of two finite sets
• Cartesian product of the reals with itself, definition of relation, pictorial diagrams, domain, codomain and range of a relation, types of relations, one-one, many-one, 
• Binary equivalence relation
• Functions – function as a special kind of relation, pictorial representation of a function, domain, codomain and range of a function, equal functions
• Types of functions - constant function, identity function, one-one function, onto function, into function, even & odd functions, polynomial function, rational function, modulus function

Probability

• Types of events – events and algebra of events, axiomatic definition of probability, mutually exclusive and exhaustive events, mutually exclusive events
• Addition theorem – for any two events A and B, Result on complementary events
• Conditional probability – definition, multiplication theorem, independent events
• Baye’s theorem, odds in favour and against

Sequences and Series

• Sequence
• A.P., Sum of first n terms of A.P., properties of A.P
• Geometric progression – introduction, general term, sum of the first ‘n’ terms, containing finitely many terms & sum to infinite terms
• Properties of G.P., H.P. as a special type of A.P
• Means – arithmetic mean, geometric mean, harmonic mean, relation between A.M., G.M., H.M
• Arithmetico-Geometric sequence, special series, sum of cube of first n natural numbers, sum of cube of first and odd natural numbers.

Also Read: How to Prepare for MHT CET in 10 Days?

MHT CET Maths Class 12th Topics 2025

The topics mentioned below are covered in the 12th standard and will be included in the Maths syllabus:

Mathematical Logic

• Sentences and statement, truth value of statement, open sentences, compound statement, quantifier and quantified statements
• Logical connectives : conjunction, disjunction, negation, implication/ conditional, 84 biconditional, truth tables of compound statements
• Examples related to real life and mathematics
• Statement patterns and logical equivalence - tautology, contradiction, contingency, duality, negation of compound statement, contrapositive, converse, inverse, algebra of statements-idempotent law, associative law, commutative law, distributive law, identity law, complement law, involution law, DeMorgan’s laws
• Difference between converse, contrapositive, contradiction, application-introduction to switching circuits (simple examples)

Matrices

• Elementary transformation of a matrix revision of cofactor and minor
• Elementary row transformation
• Elementary column transformation
• Inverse of a matrix existence and uniqueness of inverse of a matrix
• Inverse by elementary transformation
• Adjoint method
• Application-solution of the system of linear equations by – reduction method, inversion method.

Trigonometric functions

• Trigonometric equations-general solution of trigonometric equation of the type : sinθ, = 0, cosθ = 0, tanθ = 0, sinθ = sinα, cosθ = cosα, tanθ = tanα, sin2 θ = sin2 α, cos2 θ = cos2 α, tan2 θ = tan2 α, acosθ + bsinθ = C.
• Solution of a triangle : polar coordinates, sine rule, cosine rule, projection rule, area of a triangle, application
• Hero’s formula
• Napier Analogues, inverse trigonometric functions-definitions, domain, range, principle values
• Graphs of inverse trigonometric functions, properties of inverse functions.

Linear programming problems

• Introduction of L.P.P. definition of constraints
• Objective function, optimization, constraint equations, nonnegativity restrictions
• Feasible and infeasible region, feasible solutions
• Mathematical formulation-mathematical formulation of L.P.P. different types of L.P.P. problems, graphical solutions for problems in two variables, optimum feasible solution.

Continuity

• Continuity of a function at a point : left hand limit, right hand limit
• Definition of continuity of a function at a point, discontinuity of a function
• Types of discontinuity, algebra of continuous functions, continuity in interval-definition, continuity of some standard functions polynomial, rational, trigonometric, exponential and logarithmic function

Differentiation

• Revision of derivative
• Relationship between continuity and differentiability-left hand derivative and right hand derivative (need and concept)
• Every differentiable function is continuous but converse is not true
• Derivative of 86 composite function-chain rule, derivative of inverse function
• Derivative of inverse trigonometric function : Derivative of implicit function definition and examples, derivative of parametric function – definition of parametric function , exponential and logarithmic functions derivative of functions which are expressed in one of the following form a) product of functions, b) quotient of functions, c) higher order derivative, second order derivative

Applications of derivative

• Geometrical application-tangent and normal at a point
• Rolle's theorem, and Mean value theorem and their geometrical interpretation (without proof), derivative as a rate measure-introduction, increasing and decreasing function, approximation
• Maxima and minima introduction of extreme and extreme values, maxima and minima in a closed interval, first derivative test, second derivative test.

Integration

• Indefinite integrals-methods of integration, substitution method, integrals of the various types
• Integration by parts (reduction formulae are not expected), integration by partial fraction-factors involving repeated and non-repeated linear factors
• Non-repeated quadratic factors, definite integral-definite integral as a limit of sum
• Fundamental theorem of integral calculus (without proof), evaluation of definite integral 1) by substitution, 2) integration by parts, properties of definite integrals

Applications of Definite Integral

• Area under the curve : area bounded by curve and axis (simple problems), area bounded by two curves
• Volume of solid of revolution-volume of solid obtained by revolving the area under the curve about the axis (simple problems)

Pair of Straight Lines

• Pair of lines passing through origin combined equation, homogeneous equation, theorem-the joint equation of a pair of lines passing through origin and its converse
• Acute angle between the lines represented by ax2 +2hxy+by2 =0
• Condition for parallel lines, condition for perpendicular lines, pair of lines not passing through origin-combined equation of any two lines
• Condition of parallel and perpendicular lines, point of intersection of two lines

Circle

• Tangent of a circle-equation of a tangent at a point to 1) standard circle,2) general circle, condition of tangency only for line y = mx + c to the circle x2 + y2 = a2
• Tangents to a circle from a point outside the circle, director circle, length of tangent segments, normal to a circle-equation of normal at a point.

Conics

• Tangents and normals-equations of tangent and normal at a point for parabola, ellipse, hyperbola; condition of tangency for parabola
• Ellipse, hyperbola; tangents in terms of slope for parabola, ellipse, hyperbola, tangents from a point outside conics
• Locus of points from which two tangents are mutually perpendicular, properties of tangents and normals to conics (without proof).

Vectors

• Revision, Collinearity and coplanarity of vectors : linear combination of vectors, condition of collinearity of two vectors, conditions of coplanarity of three vectors
• Section formula : section formula for internal and external division, midpoint formula, centroid formula
• Scalar triple product : definition, formula, properties, geometrical interpretation of scalar triple product
• Application of vectors to geometry medians of a triangle are concurrent, altitudes of a triangle are concurrent, angle bisectors of a triangle are concurrent
• Diagonals of a parallelogram bisect each other and converse
• Median of trapezium is parallel to the parallel sides and its length is half the sum of parallel sides
• Angle subtended on a semicircle is the right angle.

Three-Dimensional Geometry

• Direction cosines and direction ratios: direction angles, direction cosines, direction ratios
• Relation between direction ratio and direction cosines, angle between two lines
• Condition of perpendicular lines

Line

• Equation of line passing through given point and parallel to given vector
• Equation of line passing through two given points
• Distance of a point from a line, distance between two skew lines, distance between two parallel lines (vector approach).

Plane

• Equation of plane in normal form, equation of plane passing through the given point and perpendicular to given vector
• Equation of plane passing through the given point and parallel to two given vectors, equation of plane passing through three noncollinear points
• Equation of plane passing through the intersection of two given planes
• Angle between two planes, angle between line and plane, condition for the coplanarity of two lines, distance of a point from a plane (vector approach)

Probability Distribution

• Probability distribution of a random variable-definition of a random variable
• Discrete and continuous random variable, probability mass function (p.m.f.), probability distribution of a discrete random variable
• Cumulative probability distribution of a discrete random variable, 87 expected value, variance and standard deviation of a discrete random variable
• Probability density function (p.d.f.), distribution function of a continuous random variable

Bernoulli Trials and Binomial Distribution

• Definition of Bernoulli trial, conditions for Binomial distribution, binomial distribution (p.m.f.), mean, variance and standard deviation
• Calculation of probabilities (without proof)
• Normal distribution : p.d.f., mean, variance and standard deviation, standard normal variable, simple problems (without proof)

MHT CET Exam Pattern 2025

It is advised to go through the MHT CET Exam Pattern thoroughly before the exam. As it can help understand the critical part of the syllabus. The exam pattern is different for the PCM and PCB courses. The details are given in the below:

MHT CET Exam Pattern for PCM 2025

The MHT CET Maths syllabus 2025 section of the exam will only include the course adopted by the candidate is PCM. The exam pattern is given in detail below:

• The MHT CET exam for PCM will include 3 sections- Physics, Chemistry and Mathematics. 
• Each section will have around 50 multiple-choice questions. 
• Candidates can take the exam in the language of their choice.
• The questions in the maths section of the exam carry 2 marks, rest of the sections carry only one mark each.
• There is no negative marking for incorrect answers.

The marking for the sections is given in the table below:

Subjects	Number of Questions	Marking for Questions
Physics	50	1
Chemistry	50	1
Mathematics	50	2

Also Read: Is There Negative Marking in MHT CET?

MHT CET Maths Topic-Wise Weightage 2025

The weightage of every topic in the MHT CET Mathematics syllabus is given below for the candidates:

Topics	Weightage
Linear Programming Problems	2%
Line	3%
Statistics	3%
Mathematical Logic	3%
Plane	4%
Bernoulli Trials And Binomial Distribution	4%
Pair Of Straight Lines	5%
Applications of Derivatives	5%
Continuity	5%
Matrices	5%
Circles	6%
Differential Equations	6%
Differentiation	7%
Vectors	7%
Three-Dimensional Geometry	8%
Trigonometric Functions	8%
Integration	9%

MHT CET Maths Marking Scheme 2025

The marking scheme of the maths syllabus for MHT CET is mentioned in the table. The whole paper will be considered for 100 marks. Each correct answer will be rewarded two marks.

However, candidates can relax on one matter without negative marking or marking for unattempted questions. 

Class	Weightage	Total Questions	Marks
XI	10%	10	20 (10x2)
XII	40%	40	80 (40x2)

Study Material for MHT CET Maths Syllabus Preparation 2025

Selecting the recommended books by experts can help candidates prepare better for the exam. The name of the books are mentioned in the table given below:

Name of the book	Author’s Name
Mathematics for MHT CET	Marvel Publication
Complete Reference Manual MHT CET Mathematics by	Arihant Publication
Pradnya’s Objective Mathematics	C.S. Patil

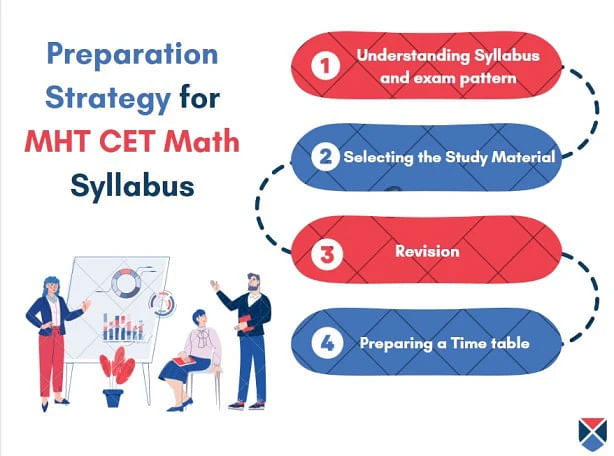
Preparation Strategy for MHT CET Maths Syllabus 2025

Candidates require good preparation for the MHT CET exam by going through the MHT CET Maths syllabus 2025 and study material available through different resources. Free preparation strategies are given below for the candidates:

• Understanding Syllabus and Exam Pattern: It is necessary to understand the MHT CET exam pattern and syllabus in order to prepare for the exam. Through this knowledge, new strategies can be formulated.
• Study Material: Selecting the right and recommended material can change the way candidates prepare for the exam. Certain topics might not be covered in a few. A few online resources for MHT CET preparation such as previous year question papers, YouTube videos and many more can help.
• Revision: It is important to not forget what is learned by doing revision again and again. Attempting mock tests and solving sample papers can help in preparation.
• Preparing a Timetable: Candidates can prepare effectively with a timetable as it helps in covering the syllabus, previous year's question papers and the revision.